Physics-Informed Neural Networks

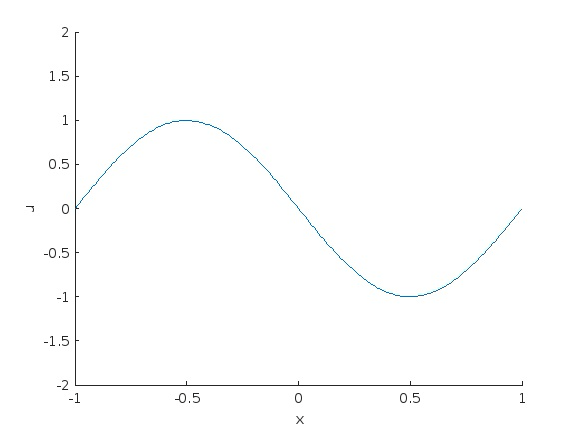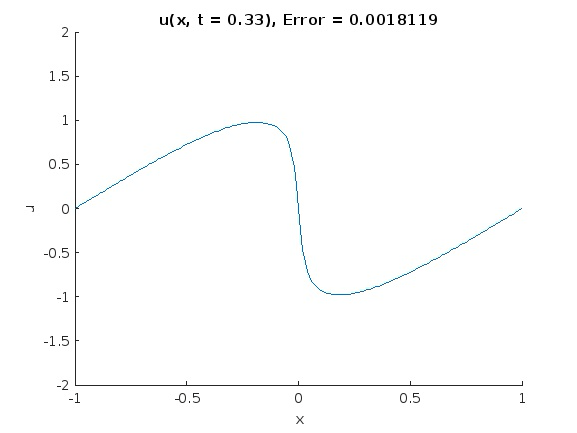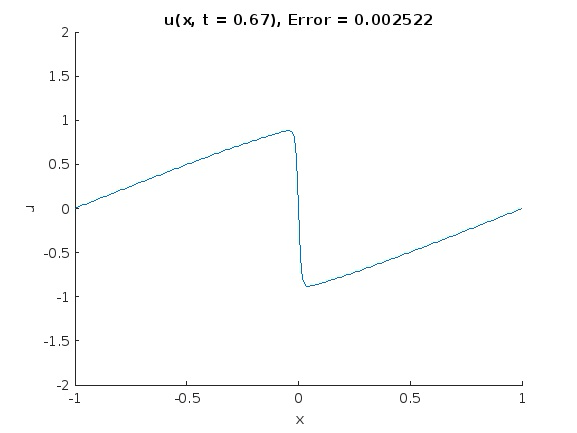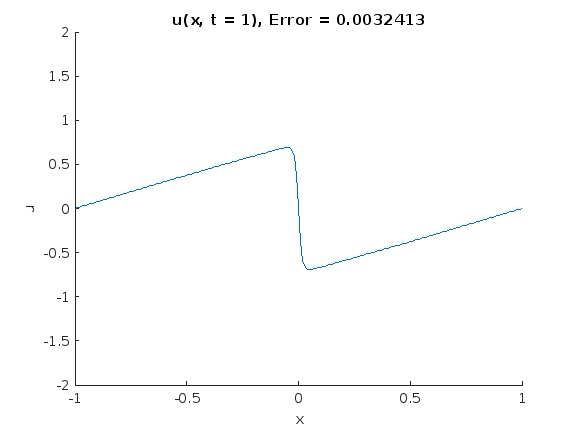
In this project for MAT 555 - Industrial Practicum, I led a team to study the use of physics-informed neural networks (PINNs) to solve an initial and boundary value problem (IBVP) governed by the 1D viscous Burgers' equation. Starting from example code provided by MATLAB, we examined the effects of network structure, activation functions, learning rate, batch size, and more on the network output.

Error at the final time vs. number of layers and neurons with the Swish activation function after 1,000 epochs. The activation function for each layer had a learnable parameter affecting the shape of Swish for that layer.

We also compared our results with those obtained from a standard explicit finite difference method, and found that the neural network is unconditionally stable whereas the standard finite difference method requires careful tuning to achieve accurate results. However, the robustness of PINNs come at a large training cost, albeit one that could be significantly reduced by training in parallel (GPU training was not available for our experiments).

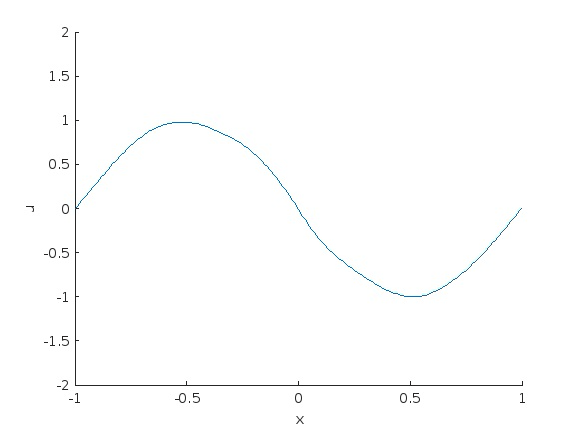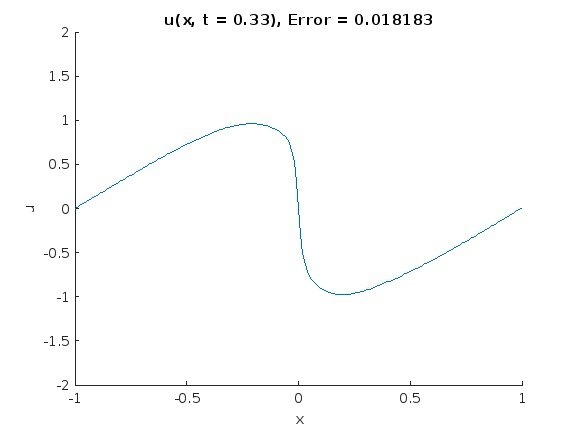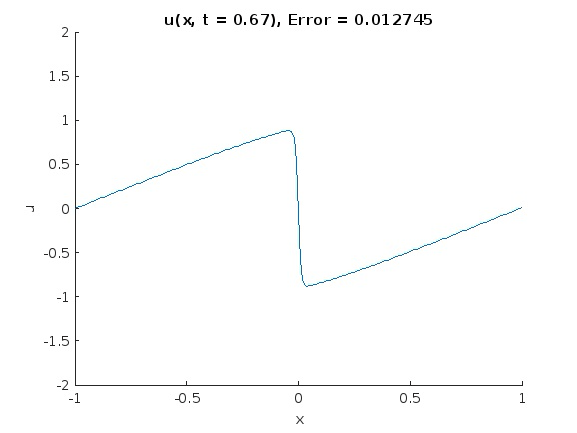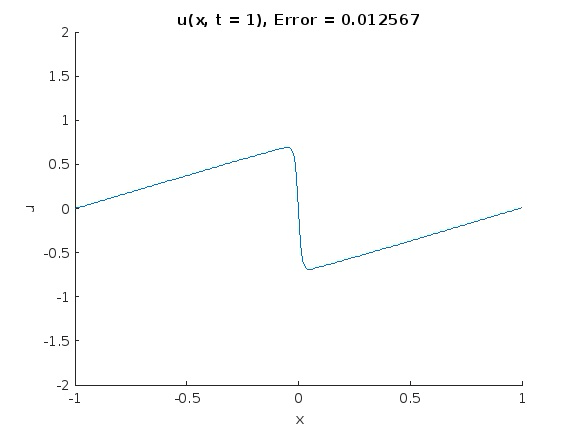
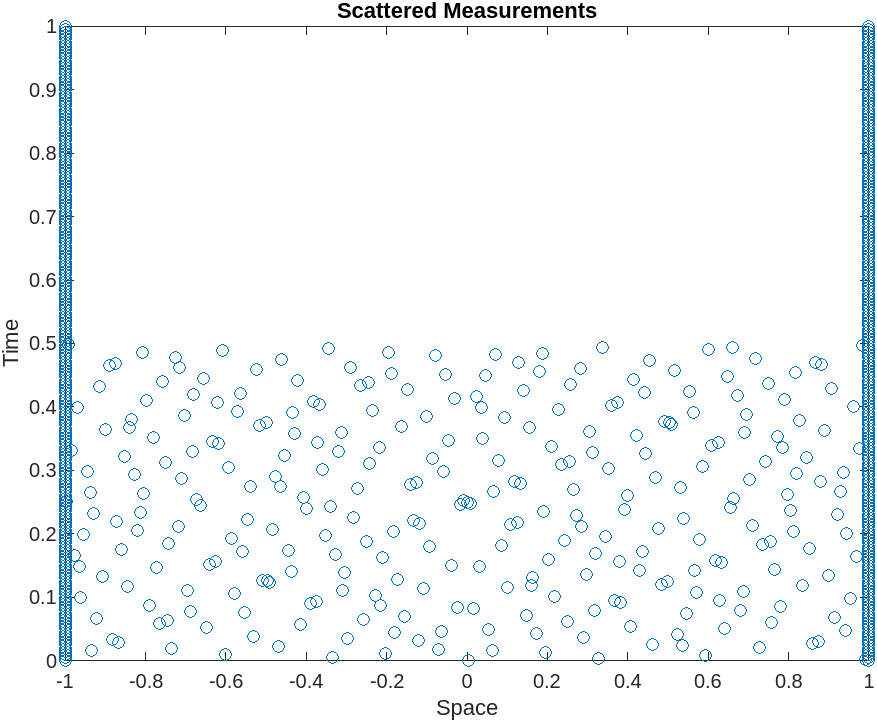
Evolution of the solution over time with incomplete initial condition.

Scattered measurements generated from the analytical solution to the IBVP used to train the network.

Interestingly, it seems that PINNs can deliver a reasonable approximation to the solution of the IBVP even with an incomplete initial condition, which suggests PINNs as a useful technique for extrapolating from scattered data.

I was awarded first prize for my oral presentation on this project at the WCU Research and Creative Activity day on April 17th, 2024. For more information, click here.

Source code, slides, and report can be found in the repo.