1D Layout Optimization

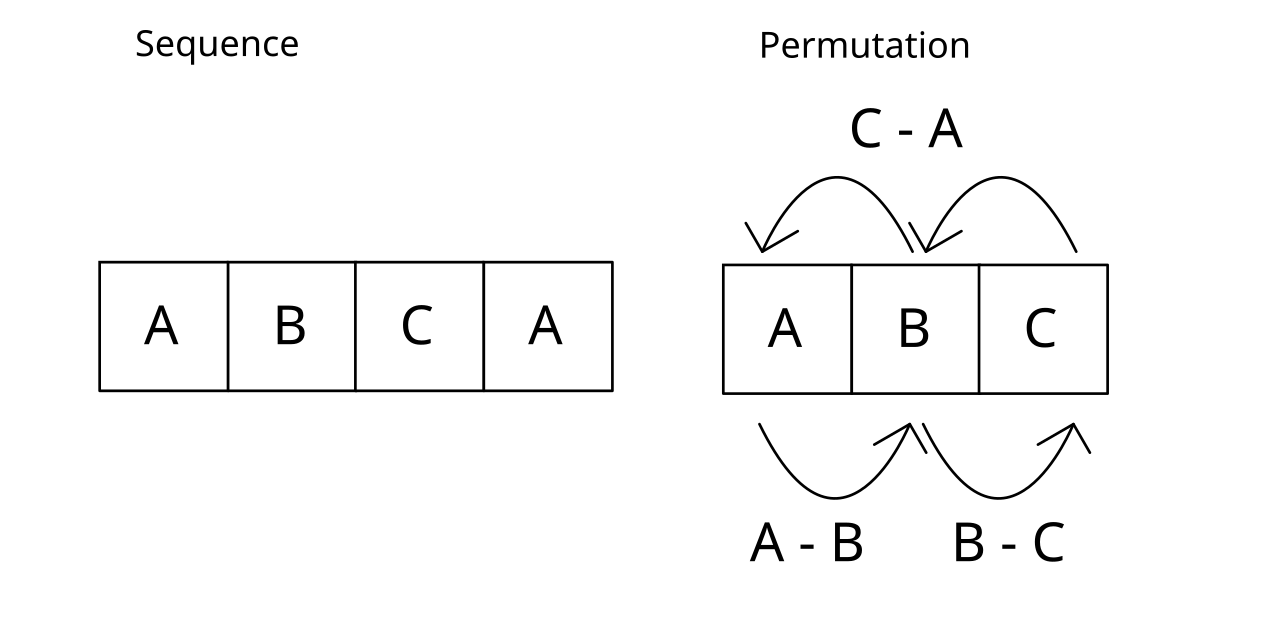
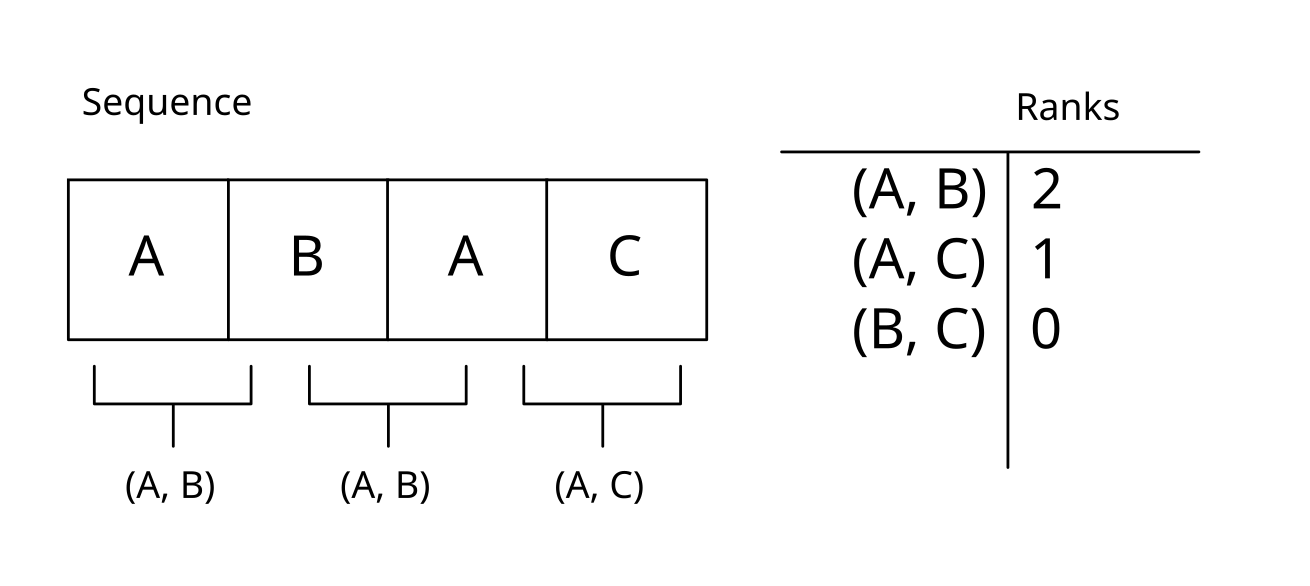
In this project for MAT 552 - Operations Research, I designed a method to find a layout of locations that minimizes the total distance traveled for a given route across them with repeat visits in 1 dimension. The problem was originally envisioned as a method for profile-guided optimization in a compiler, the idea being that functions or data could be automatically placed in memory to maximize cache locality for a known access pattern. However, I was also interested in the problem as a sort of inversion of the traveling salesman problem. In the TSP, the locations are fixed and the goal is to find the route; in my problem, the route is fixed and the goal is to find the locations.

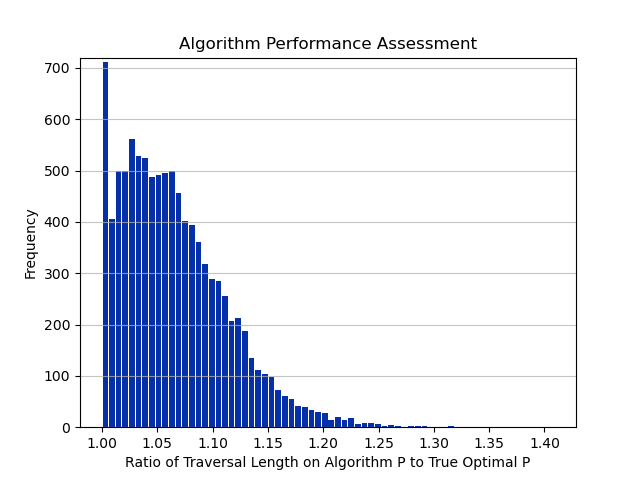
Illustration of the basic idea behind the method: the points most frequently moved between are given a high rank, so the algorithm prioritizes placing them together.

The performance of the method compared to brute force search in 10,000 runs with random traversal sequences. The algorithm is able to quickly find near-optimal layouts in nearly all cases.

Source code, slides, and report can be found in the repo.