In this project for MAT 325 - Numerical Analysis, I developed a method to sample and parameterize closed implicit (level-set) curves. Often, there are simple and convenient implicit representations for shapes. Beyond simplicity, implicit representations are also useful for applications such as constructive solid geometry. However, a parametric representation is convenient for other applications, such as integrating along a boundary. The goal of this project was to enable simple conversion from implicit representations to parametric representations.
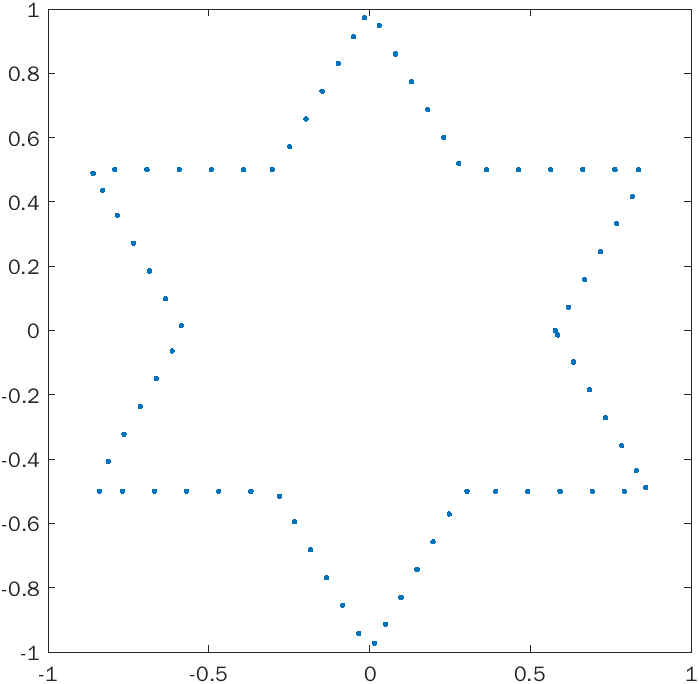
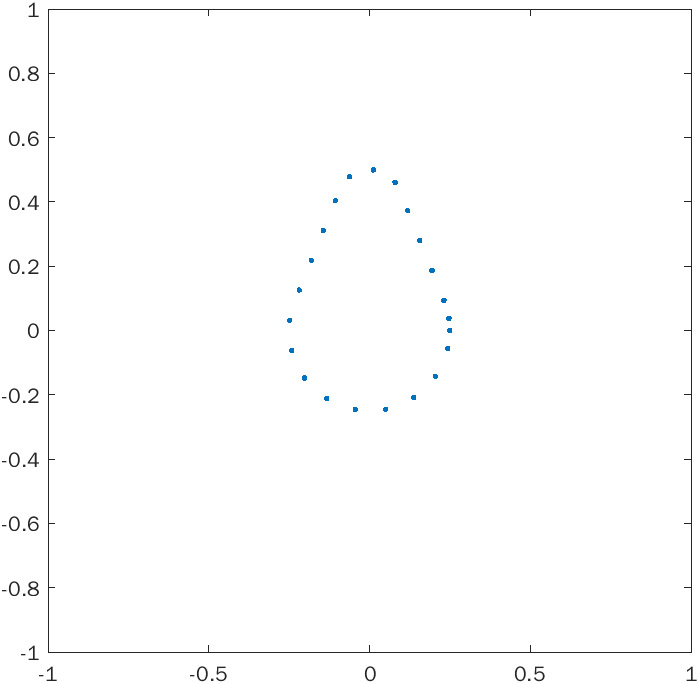
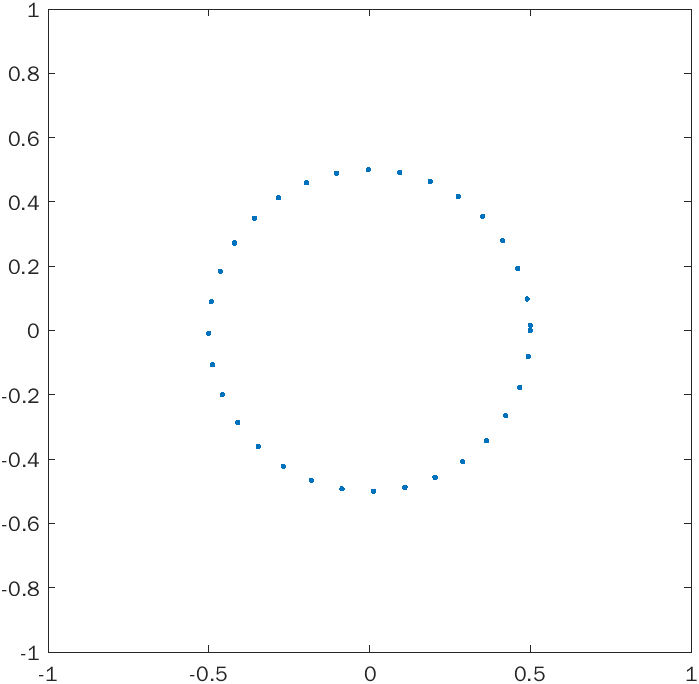
The method consists of two parts. First, the implicit curve must be sampled in such a way that the sample points lie sequentially counter-clockwise around the curve. To do this, a point on the curve is first found by a variant of Newton's method. Then, the tangent line to the curve is found by using the fact that the gradient is perpendicular to the level curve. A new point is created a short distance away along this line, then it is moved onto the curve using Newton's method again. Then a tangent line is created at this new point and the process repeats.
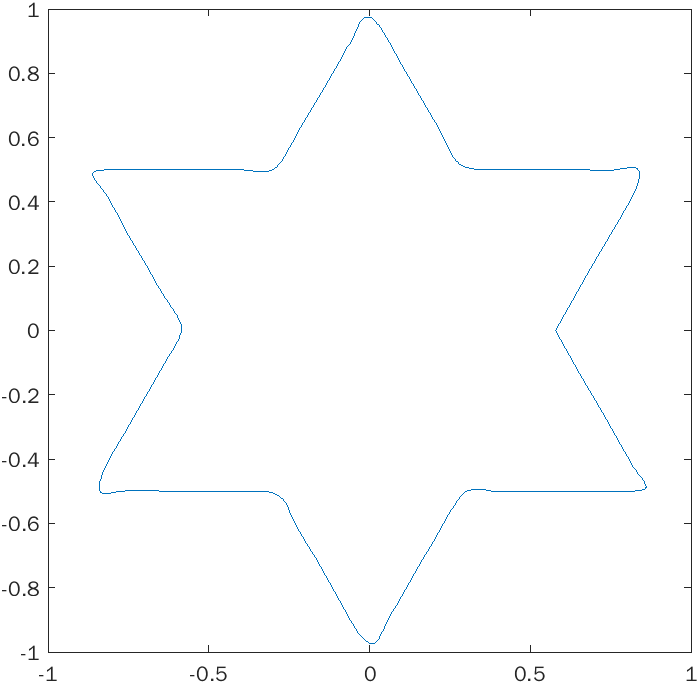
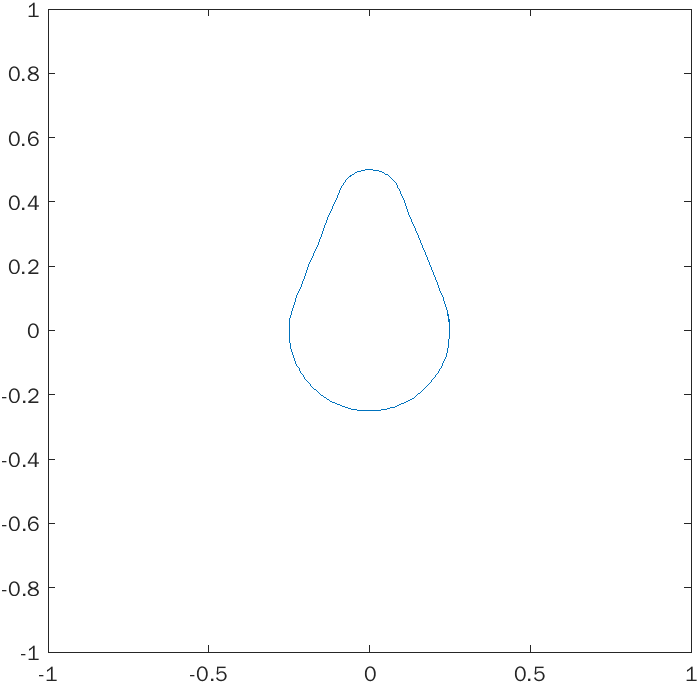
Second, the sampled points must be interpolated. As per the project requirements, I used parametric cubic splines and parametric Lagrange interpolation, however the latter did not work very well. The poor performance of the Lagrange interpolation was to be expected, as a large number of sample points must be interpolated. Cubic splines performed reasonably well, however they have difficulty with sharp corners on the shapes. This could be remedied by using adaptive sampling in the first step, however I did not have time to implement this.
Source code and report can be found in the repo.